昨天有深度,今天有廣度,人生難過沒法度~ (好難笑...呵呵)
今天就用這張圖來開啟主題。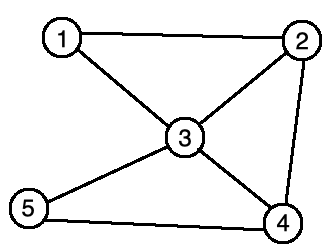
這是一個無向圖,比較接近現實中的地圖。今天我們要從 1 號城市搭飛機到 5 號城市,請問要怎麼搭轉機次數最少呢?
當然,我們用看的就可以知道先從 1 號飛到 3 號,再飛到 5 號,但電腦要怎麼判別?
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | ∞ | ∞ |
| 2 | 1 | 0 | 1 | 1 | ∞ |
| 3 | 1 | 1 | 0 | 1 | 1 |
| 4 | ∞ | 1 | 1 | 0 | 1 |
| 5 | ∞ | ∞ | 1 | 1 | 0 |
首先可以從 1 號到達 2 號和 3 號城市。
| x | 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|---|
| step | 0 | 1 | 1 | ||||
| 2 號城市又可以到達 3 號和 4 號城市,但 3 號已經在佇列中,所以只需將 4 號加入到佇列。 | |||||||
| x | 1 | 2 | 3 | 4 | |||
| - | - | - | - | - | - | - | - |
| step | 0 | 1 | 1 | 2 | |||
| 接著 3 號城市又可以到達 4 號城市和 5 號城市,因為 4 號也已經在佇列中,所以只需將 5 號加入。 | |||||||
| x | 1 | 2 | 3 | 4 | 5 | ||
| - | - | - | - | - | - | - | - |
| step | 0 | 1 | 1 | 2 | 2 | ||
| 找到 5 號城市,演算法就結束啦。可以想一想,為什麼一擴展到 5 號城市就可以結束,而之前的深度優先搜尋卻不行呢? (答案我不告訴你,哈哈) |
import numpy as np
'''
輸入驗證資料:
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
'''
class note:
def __init__(self):
self.x = np.zeros(2501, dtype=np.int) #城市編號
self.s = np.zeros(2501, dtype=np.int) #轉機次數
que = note()
book = np.zeros(51, dtype=np.int)
e = np.zeros((51,51), dtype=np.int)
flag = 0
n, m, start, end = map(int, input().split(' '))
# 初始化二維矩陣
for i in range(1, n+1):
for j in range(1, n+1):
if i==j:
e[i][j]=0
else:
e[i][j]=99999999
#讀入城市間的航班
for i in range(1, m+1):
a, b = map(int, input().split(' '))
#這邊是無相圖!!!
e[a][b]=1
e[b][a]=1
#佇列初始化
head = 1
tail = 1
#從start城市出發,並加入到佇列
que.x[tail] = start
que.s[tail] = 0
tail += 1
book[1] = start #標記已加入佇列中
#當佇列不為空
while head<tail :
cur = que.x[head] #目前佇列中首城市的編號
for j in range(1, n+1): #從1~n依次嘗試
#判斷從城市cur到城市j是否有航班,並判斷城市j是否已經在佇列中
if e[cur][j] != 99999999 and book[j]==0 :
#如果從城市cur到城市j有航班且城市j不在佇列中,則將j城市加入佇列
que.x[tail] = j
que.s[tail] = que.s[head] +1 #轉機次數+1
tail +=1
book[j]=1 #標記城市已在佇列中
#如果到達目標城市,停止擴展,任務結束,退出迴圈
if que.x[tail] == end:
flag = 1
break
if flag ==1:
break
# 當一個擴展結束後,要head++才能對後面的點再進行擴展
head += 1
# 列印佇列中末尾最後一個點(目標城市)的步數,但tail是指向佇列尾的下一個位置,所以要-1
print (que.s[tail-1])
其實用深度優先搜尋也是可以解決問題的,但這邊用廣度優先搜尋會比較快。因為廣度優先搜尋比較適合用在所有邊的權重都相同的情況。
